ControlSystemsBase.bodeplotControlSystemsBase.gangoffourplotControlSystemsBase.marginplotControlSystemsBase.nicholsplotControlSystemsBase.nyquistplotControlSystemsBase.pzmapControlSystemsBase.rgaplotControlSystemsBase.setPlotScaleControlSystemsBase.sigmaplot
All plotting requires the user to manually load the Plots.jl library, e.g., by calling using Plots.
Plotting functions
ControlSystemsBase.bodeplot — Functionfig = bodeplot(sys, args...)
bodeplot(LTISystem[sys1, sys2...], args...; plotphase=true, balance = true, kwargs...)Create a Bode plot of the LTISystem(s). A frequency vector w can be optionally provided. To change the Magnitude scale see setPlotScale. The default magnitude scale is "log10" (absolute scale).
- If
hz=true, the plot x-axis will be displayed in Hertz, the input frequency vector is still treated as rad/s. balance: Callbalance_statespaceon the system before plotting.
kwargs is sent as argument to RecipesBase.plot.
ControlSystemsBase.gangoffourplot — Methodfig = gangoffourplot(P::LTISystem, C::LTISystem; minimal=true, plotphase=false, Ms_lines = [1.0, 1.25, 1.5], Mt_lines = [], sigma = true, kwargs...)Gang-of-Four plot.
sigma determines whether a sigmaplot is used instead of a bodeplot for MIMO S and T. kwargs are sent as argument to RecipesBase.plot.
ControlSystemsBase.marginplot — Functionfig = marginplot(sys::LTISystem [,w::AbstractVector]; balance=true, kwargs...)
marginplot(sys::Vector{LTISystem}, w::AbstractVector; balance=true, kwargs...)Plot all the amplitude and phase margins of the system(s) sys.
- A frequency vector
wcan be optionally provided. balance: Callbalance_statespaceon the system before plotting.
kwargs is sent as argument to RecipesBase.plot.
ControlSystemsBase.nicholsplot — Functionfig = nicholsplot{T<:LTISystem}(systems::Vector{T}, w::AbstractVector; kwargs...)Create a Nichols plot of the LTISystem(s). A frequency vector w can be optionally provided.
Keyword arguments:
text = true
Gains = [12, 6, 3, 1, 0.5, -0.5, -1, -3, -6, -10, -20, -40, -60]
pInc = 30
sat = 0.4
val = 0.85
fontsize = 10pInc determines the increment in degrees between phase lines.
sat ∈ [0,1] determines the saturation of the gain lines
val ∈ [0,1] determines the brightness of the gain lines
Additional keyword arguments are sent to the function plotting the systems and can be used to specify colors, line styles etc. using regular RecipesBase.jl syntax
This function is based on code subject to the two-clause BSD licence Copyright 2011 Will Robertson Copyright 2011 Philipp Allgeuer
ControlSystemsBase.nyquistplot — Functionfig = nyquistplot(sys; Ms_circles=Float64[], Mt_circles=Float64[], unit_circle=false, hz=false, critical_point=-1, kwargs...)
nyquistplot(LTISystem[sys1, sys2...]; Ms_circles=Float64[], Mt_circles=Float64[], unit_circle=false, hz=false, critical_point=-1, kwargs...)Create a Nyquist plot of the LTISystem(s). A frequency vector w can be optionally provided.
unit_circle: if the unit circle should be displayed. The Nyquist curve crosses the unit circle at the gain crossover frequency.Ms_circles: draw circles corresponding to given levels of sensitivity (circles around -1 with radii1/Ms).Ms_circlescan be supplied as a number or a vector of numbers. A design staying outside such a circle has a phase margin of at least2asin(1/(2Ms))rad and a gain margin of at leastMs/(Ms-1).Mt_circles: draw circles corresponding to given levels of complementary sensitivity.Mt_circlescan be supplied as a number or a vector of numbers.critical_point: point on real axis to mark as critical for encirclements- If
hz=true, the hover information will be displayed in Hertz, the input frequency vector is still treated as rad/s. balance: Callbalance_statespaceon the system before plotting.
kwargs is sent as argument to plot.
ControlSystemsBase.pzmap — Functionfig = pzmap(fig, system, args...; hz = false, kwargs...)Create a pole-zero map of the LTISystem(s) in figure fig, args and kwargs will be sent to the scatter plot command.
To customize the unit-circle drawn for discrete systems, modify the line attributes, e.g., linecolor=:red.
If hz is true, all poles and zeros are scaled by 1/2π.
ControlSystemsBase.rgaplot — Functionrgaplot(sys, args...; hz=false)
rgaplot(LTISystem[sys1, sys2...], args...; hz=false, balance=true)Plot the relative-gain array entries of the LTISystem(s). A frequency vector w can be optionally provided.
- If
hz=true, the plot x-axis will be displayed in Hertz, the input frequency vector is still treated as rad/s. balance: Callbalance_statespaceon the system before plotting.
kwargs is sent as argument to Plots.plot.
ControlSystemsBase.setPlotScale — MethodsetPlotScale(str)Set the default scale of magnitude in bodeplot and sigmaplot. str should be either "dB" or "log10". The default scale if none is chosen is "log10".
ControlSystemsBase.sigmaplot — Functionsigmaplot(sys, args...; hz=false balance=true, extrema)
sigmaplot(LTISystem[sys1, sys2...], args...; hz=false, balance=true, extrema)Plot the singular values of the frequency response of the LTISystem(s). A frequency vector w can be optionally provided.
- If
hz=true, the plot x-axis will be displayed in Hertz, the input frequency vector is still treated as rad/s. balance: Callbalance_statespaceon the system before plotting.extrema: Only plot the largest and smallest singular values.
kwargs is sent as argument to Plots.plot.
Examples
Bode plot

tf1 = tf([1],[1,1])
tf2 = tf([1/5,2],[1,1,1])
sys = [tf1 tf2]
ws = exp10.(range(-2,stop=2,length=200))
bodeplot(sys, ws)Sigma plot
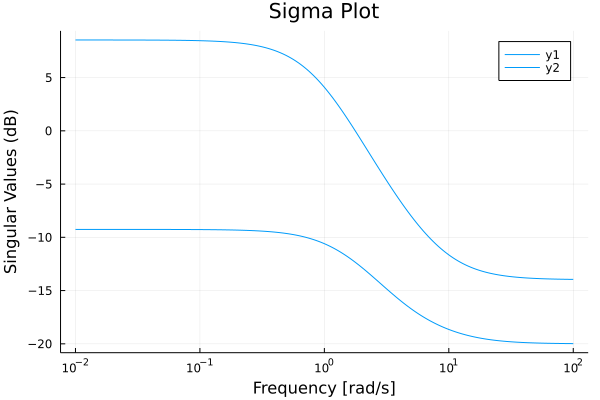
sys = ss([-1 2; 0 1], [1 0; 1 1], [1 0; 0 1], [0.1 0; 0 -0.2])
sigmaplot(sys)Margin

tf1 = tf([1],[1,1])
tf2 = tf([1/5,2],[1,1,1])
ws = exp10.(range(-2,stop=2,length=200))
marginplot([tf1, tf2], ws)Gangoffour plot
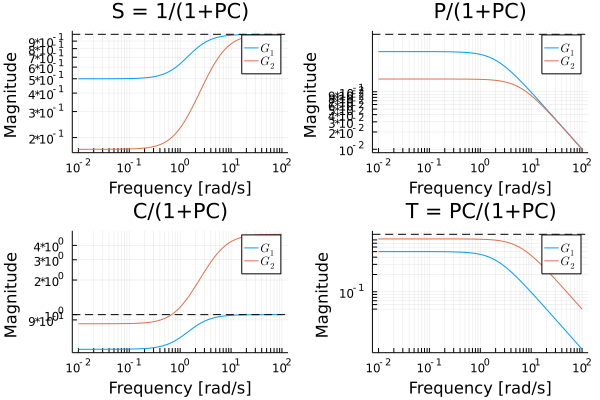
tf1 = tf([1.0],[1,1])
gangoffourplot(tf1, [tf(1), tf(5)])Nyquist plot

sys = ss([-1 2; 0 1], [1 0; 1 1], [1 0; 0 1], [0.1 0; 0 -0.2])
ws = exp10.(range(-2,stop=2,length=200))
nyquistplot(sys, ws, Ms_circles=1.2, Mt_circles=1.2)Nichols plot
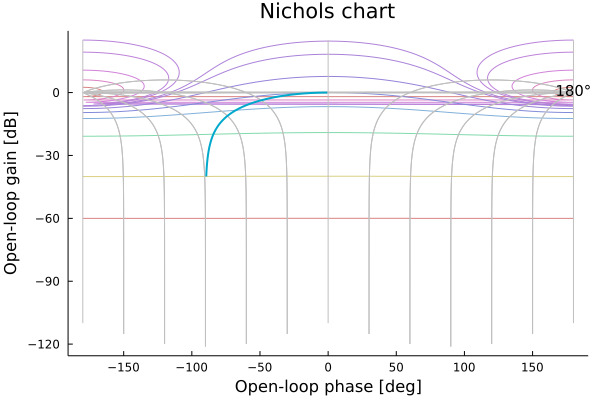
tf1 = tf([1],[1,1])
ws = exp10.(range(-2,stop=2,length=200))
nicholsplot(tf1,ws)Pole-zero plot
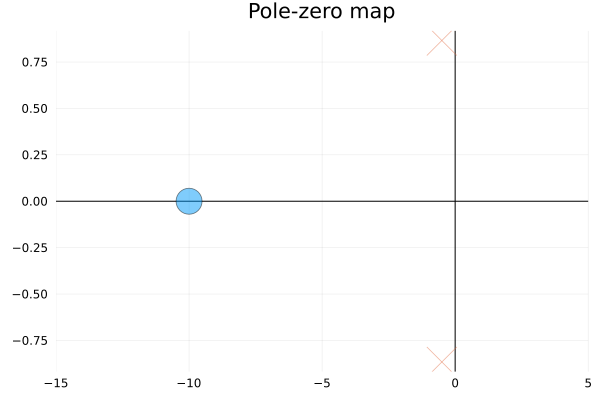
tf2 = tf([1/5,2],[1,1,1])
pzmap(c2d(tf2, 0.1))Rlocus plot
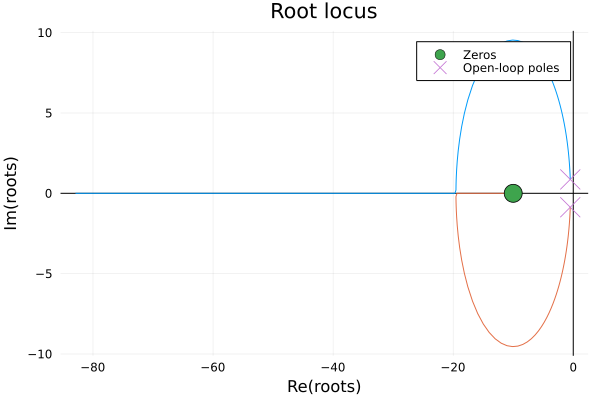
Lsim response plot

sys = ss([-1 2; 0 1], [1 0; 1 1], [1 0; 0 1], [0.1 0; 0 -0.2])
sysd = c2d(sys, 0.01)
L = lqr(sysd, [1 0; 0 1], [1 0; 0 1])
ts = 0:0.01:5
plot(lsim(sysd, (x,i)->-L*x, ts; x0=[1;2]), plotu=true)Impulse response plot
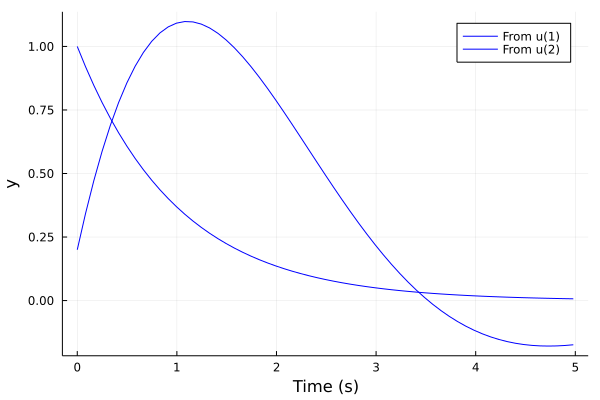
tf1 = tf([1],[1,1])
tf2 = tf([1/5,2],[1,1,1])
sys = [tf1 tf2]
sysd = c2d(ss(sys), 0.01)
plot(impulse(sysd, 5), l=:blue)Step response plot
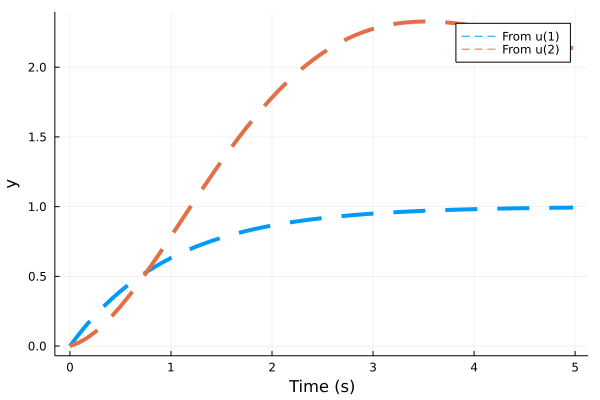
tf1 = tf([1],[1,1])
tf2 = tf([1/5,2],[1,1,1])
sys = [tf1 tf2]
sysd = c2d(ss(sys), 0.01)
res = step(sysd, 5)
plot(res, l=(:dash, 4))
# plot!(stepinfo(step(sysd[1,1], 5))) # adds extra info to the plot